Mathematics: Understanding Trigonometry

Understanding Trigonometry

Understanding Trigonometry

Mathematics: Understanding Trigonometry is a crucial topic in the IGCSE Mathematics syllabus that deals with the
relationships between angles and sides of triangles, particularly right-angled triangles. These relationships form the foundation for understanding various real-world problems, including navigation, architecture, and engineering. In this article, we will cover the basics of trigonometry, including trigonometric ratios, solving triangles, and applying trigonometry to real-life situations.

What is Trigonometry?

Trigonometry is the branch of mathematics that studies the relationships between the angles and lengths of triangles. Specifically, it focuses on right-angled triangles, where one angle is 90∘90^\circ90∘. In trigonometry, we explore how the angles of a triangle relate to the lengths of the sides.

The three main trigonometric functions, or ratios, are:

• Sine (sin): The ratio of the opposite side to the hypotenuse.
• Cosine (cos): The ratio of the adjacent side to the hypotenuse.
• Tangent (tan): The ratio of the opposite side to the adjacent side.

These ratios allow us to solve for unknown sides or angles in right-angled triangles when some information is already known.

• Introduction to Trigonometry – BBC Bitesize

Trigonometric Ratios

Mathematics: Understanding Trigonometry

The three basic trigonometric ratios are fundamental in solving problems related to triangles. Here is how they are defined for a right-angled triangle:

1. Sine:sin⁡(θ)=OppositeHypotenuse\sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}}sin(θ)=HypotenuseOpposite​The sine of an angle is the ratio between the length of the side opposite the angle and the hypotenuse.

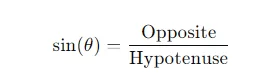
1. Cosine:cos⁡(θ)=AdjacentHypotenuse\cos(\theta) = \frac{\text{Adjacent}}{\text{Hypotenuse}}cos(θ)=HypotenuseAdjacent​The cosine of an angle is the ratio of the length of the adjacent side to the hypotenuse.

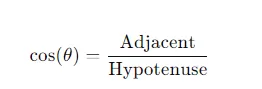
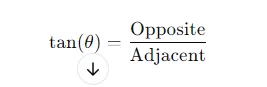
1. Tangent:tan⁡(θ)=OppositeAdjacent\tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}}tan(θ)=AdjacentOpposite​The tangent of an angle is the ratio between the side opposite the angle and the side adjacent to it.

Solving Right-Angled Triangles

Trigonometry is often used to solve right-angled triangles, where you may be required to find a missing side or angle.

1. Finding a Side: Suppose you know one angle (other than the right angle) and one side of a right-angled triangle. You can use one of the trigonometric ratios to find a missing side. For example, if you know the angle θ\thetaθ and the length of the hypotenuse, you can find the opposite side using:sin⁡(θ)=OppositeHypotenuse⇒Opposite=sin⁡(θ)×Hypotenuse\sin(\theta) = \frac{\text{Opposite}}{\text{Hypotenuse}} \quad \Rightarrow \quad \text{Opposite} = \sin(\theta) \times \text{Hypotenuse}sin(θ)=HypotenuseOpposite​⇒Opposite=sin(θ)×Hypotenuse

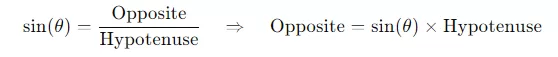
1. Finding an Angle: To find an unknown angle, you can use the inverse of the trigonometric ratios. For instance, if you know the opposite and adjacent sides, you can find the angle θ\thetaθ using:θ=tan⁡−1(OppositeAdjacent)\theta = \tan^{-1} \left( \frac{\text{Opposite}}{\text{Adjacent}} \right)θ=tan−1(AdjacentOpposite​)

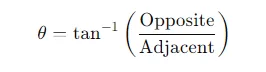
1. Pythagoras’ Theorem: Another useful tool when solving triangles is Pythagoras’ Theorem, which states that in a right-angled triangle:a2+b2=c2a^2 + b^2 = c^2a2+b2=c2where aaa and bbb are the lengths of the two legs, and ccc is the length of the hypotenuse. This theorem allows you to find the length of one side when the other two sides are known.

1. Solving Right-Angled Triangles – MathsIsFun

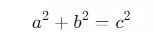
The Unit Circle and Trigonometric Functions

Beyond right-angled triangles, trigonometric functions are defined using the unit circle, a circle with a radius of 1 centered at the origin of the coordinate plane. The unit circle helps extend the definition of trigonometric functions to any angle, including those greater than 90∘90^\circ90∘.

In the unit circle: Understanding Trigonometry

• The x-coordinate of a point on the circle corresponds to the cosine of the angle.
• The y-coordinate corresponds to the sine of the angle.
• The tangent is the ratio of the sine to the cosine at any point on the circle.

This concept is crucial in advanced trigonometry and has applications in areas like physics and engineering. Understanding Trigonometry

• The Unit Circle – Varsity Tutors

Applications of Trigonometry in Real Life

Trigonometry is used in many fields, from architecture to astronomy. Some common real-life applications include: Understanding Trigonometry

1. Architecture and Engineering: Architects and engineers use trigonometry to calculate angles, lengths, and forces when designing structures such as bridges and buildings. For example, knowing the angles of inclination can help determine the height of a building or the length of a support beam.
2. Navigation: Pilots and sailors use trigonometry to determine distances and plot courses. By calculating angles based on positions and distances, trigonometry helps in navigation over both land and sea.
3. Physics and Astronomy: Trigonometry is essential for calculating the trajectories of objects, such as satellites or spacecraft, and for understanding the properties of waves, light, and sound.
   • Applications of Trigonometry – ThoughtCo

Trigonometric Identities

Trigonometric identities are equations that are true for all values of the variables involved. These identities are useful in simplifying expressions and solving trigonometric equations. Understanding Trigonometry

1. Pythagorean Identity:sin⁡2(θ)+cos⁡2(θ)=1\sin^2(\theta) + \cos^2(\theta) = 1sin2(θ)+cos2(θ)=1

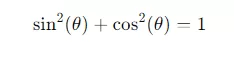
This identity is derived from the unit circle and is one of the most important identities in trigonometry.

1. Tangent Identity:tan⁡(θ)=sin⁡(θ)cos⁡(θ)\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}tan(θ)=cos(θ)sin(θ)​

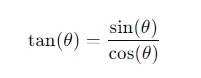
1. Reciprocal Identities:

1. Trigonometric Identities – Math Open Reference

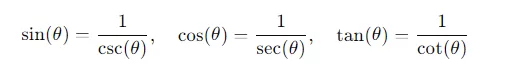
Conclusion Understanding Trigonometry

Trigonometry is a versatile and essential branch of mathematics that extends beyond the classroom and into real-world applications. By mastering the trigonometric ratios, solving triangles, and understanding the unit circle, students gain the tools needed for advanced mathematical studies and various practical applications in science, engineering, and architecture.